Compound Interest Calculator
Long-term investing can be a great way to save for your future.
Use our compound interest calculator to see how your investments will grow over time.
Effective Interest Rate: (annual)
Summary
If you start with $10,000 in a savings account earning a 7% interest rate, compounded annually, and make $100 deposits on a monthly basis, after 20 years your savings account will have grown to $89,737.45 - of which $34,000 is the total of your beginning balance plus deposits, and $55,737.45 are the total interest earnings.
Compounding Interest - Investment Analysis
| Year | Start Principal | Deposits | Yearly Interest | Total Interest | Balance |
|---|---|---|---|---|---|
| 2020 | $10,000 | $1,200 | $745.03 | $745.03 | $11,945.03 |
| 2021 | $10,000 | $2,400 | $881.18 | $1,626.21 | $14,026.21 |
| 2022 | $10,000 | $3,600 | $1,026.86 | $2,653.08 | $16,253.08 |
| 2023 | $10,000 | $4,800 | $1,182.75 | $3,835.82 | $18,635.82 |
| 2024 | $10,000 | $6,000 | $1,349.54 | $5,185.36 | $21,185.36 |
| 2025 | $10,000 | $7,200 | $1,528 | $6,713.36 | $23,913.36 |
| 2026 | $10,000 | $8,400 | $1,718.97 | $8,432.33 | $26,832.33 |
| 2027 | $10,000 | $9,600 | $1,923.29 | $10,355.62 | $29,955.62 |
| 2028 | $10,000 | $10,800 | $2,141.92 | $12,497.54 | $33,297.54 |
| 2029 | $10,000 | $12,000 | $2,375.86 | $14,873.4 | $36,873.4 |
| 2030 | $10,000 | $13,200 | $2,626.17 | $17,499.57 | $40,699.57 |
| 2031 | $10,000 | $14,400 | $2,894 | $20,393.57 | $44,793.57 |
| 2032 | $10,000 | $15,600 | $3,180.58 | $23,574.15 | $49,174.15 |
| 2033 | $10,000 | $16,800 | $3,487.22 | $27,061.37 | $53,861.37 |
| 2034 | $10,000 | $18,000 | $3,815.33 | $30,876.69 | $58,876.69 |
| 2035 | $10,000 | $19,200 | $4,166.4 | $35,043.09 | $64,243.09 |
| 2036 | $10,000 | $20,400 | $4,542.05 | $39,585.14 | $69,985.14 |
| 2037 | $10,000 | $21,600 | $4,943.99 | $44,529.13 | $76,129.13 |
| 2038 | $10,000 | $22,800 | $5,374.07 | $49,903.2 | $82,703.2 |
| 2039 | $10,000 | $24,000 | $5,834.25 | $55,737.45 | $89,737.45 |
Compounding Interval Comparison
Here's how different compounding period intervals are affecting the total amount generated and interest earned. This is because rate at which compound interest grows depends on the compounding frequency, such that the higher the compounding frequency, the greater the compound interest.
| Compound Interval | Total Amount | Interest |
|---|---|---|
| Annually (1) | $89,737.45 | $55,737.45 |
| Semi-Annually (2) | $91,353.56 | $57,353.56 |
| Quarterly (4) | $92,202.19 | $58,202.19 |
| Bi-Monthly (6) | $92,491.42 | $58,491.42 |
| Monthly (12) | $92,783.93 | $58,783.93 |
| Semi-Monthly (24) | $92,931.43 | $58,931.43 |
| Bi-Weekly (26) | $92,942.81 | $58,942.81 |
| Weekly (52) | $93,011.2 | $59,011.2 |
| Daily (365) | $93,069.99 | $59,069.99 |
Note: the calculations above do not take into account taxation, or inflation. They reflect calculations based on input provided in the compound interest calculator and are displayed for compounding periods comparison purposes.
How to use the compound interest calculator?
This compound interest calculator helps you easily identify: how much money you'll have if you save regularly; how the power of compounding increases your savings interest; what it means to start saving now vs saving later & how to calculate compound interest.
Below you can find information on how the compound interest calculator works, what user input it accepts and how to interpret the results and future value growth chart.
User Input
- Initial Principle - Amount of money that you have available to invest initially.
- Regular Deposit / Withdrawal - Amount that you plan to add to the principal every month, or a negative number for the amount that you plan to withdraw.
- Deposit / Withdrawal Frequency - How often you plan to add to your deposit or make a withdraw. This ranges from daily to yearly.
- Rate (%) - Your estimated annual interest rate.
- Years - Length of time, in years, that you plan to save.
- Compound frequency - Times per period that interest will be compounded. The compound interest calculator includes a variety of compounding periods available for you to experiment with:
- daily compounding
- weekly compounding (& bi-weekly)
- monthly compounding ( + bi-monthly & semi-monthly)
- quarterly compounding
- yearly compounding (& semi-annually)
- Tax (%) (optional) - Amount of tax in % that is paid on a yearly basis at the end of the year on interest earnings, and thus subtracted from the end of year total earnings. On / Off button allows you to calculate future gains with or without tax.
- Inflation (%) (optional) - Inflation-adjusted return reveals the return on an investment after removing the effects of inflation. Removing the effects of inflation from the return of an investment allows the investor to see the true earning potential of the security without external economic forces. On / Off button allows you to display future gains that are inflation adjusted.
Growth chart interpretation
- Principal - displayed with gray color bars on the chart
- Deposit / Withdrawal - these are represented on the chart using the following colors:
- green color bars (in case of deposits)
- yellow color bars (in case of withdrawals)
- red color bars (in case the withdrawals are greater than the earned interest)
- Interest - displayed with blue color bars on the chart
- Tax - displayed with violet / magenta color bars on the chart
- Inflation Adjusted - displayed with red line on the chart
You can how over the chart bars to see individual metrics for any of the calculated yearly time series.
What Is Compound Interest?
Compound interest (or compounding interest) is interest calculated on the initial principal, which also includes all the accumulated interest of previous periods of a deposit.
Compound interest is calculated by multiplying the initial principal amount by one plus the annual interest rate raised to the number of compound periods minus one.
How Compound Interest Grows Over Time
If you invested $10,000 which compounded annually at 7%, it would be worth over $76,122.55 after 30 years, accruing over $66,122.55 in compounded interest. More so if you look at the graph below, the benefits of compound interest outweigh standard interest by $45,122.55.
Here we compare the benefits of compound interest versus standard interest and no interest at all.
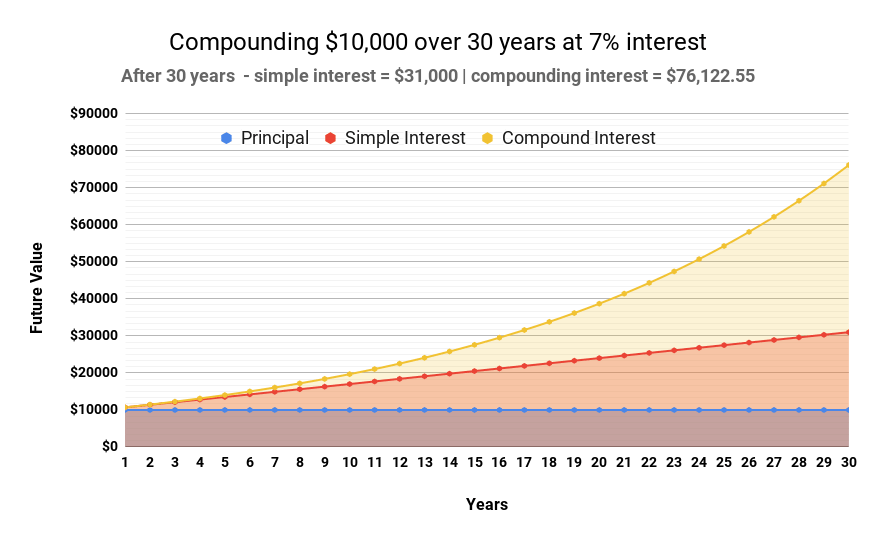
The Effect of Compounding Periods
Interest can be compounded on any given frequency schedule, from continuous to daily, monthly, quarterly to annually. When calculating compound interest, the number of compounding periods makes a significant difference for future earnings.
The following chart demonstrates the difference that the number of compounding periods can make for a $10,000 investment with an annual 7% interest rate over a 10-year period.
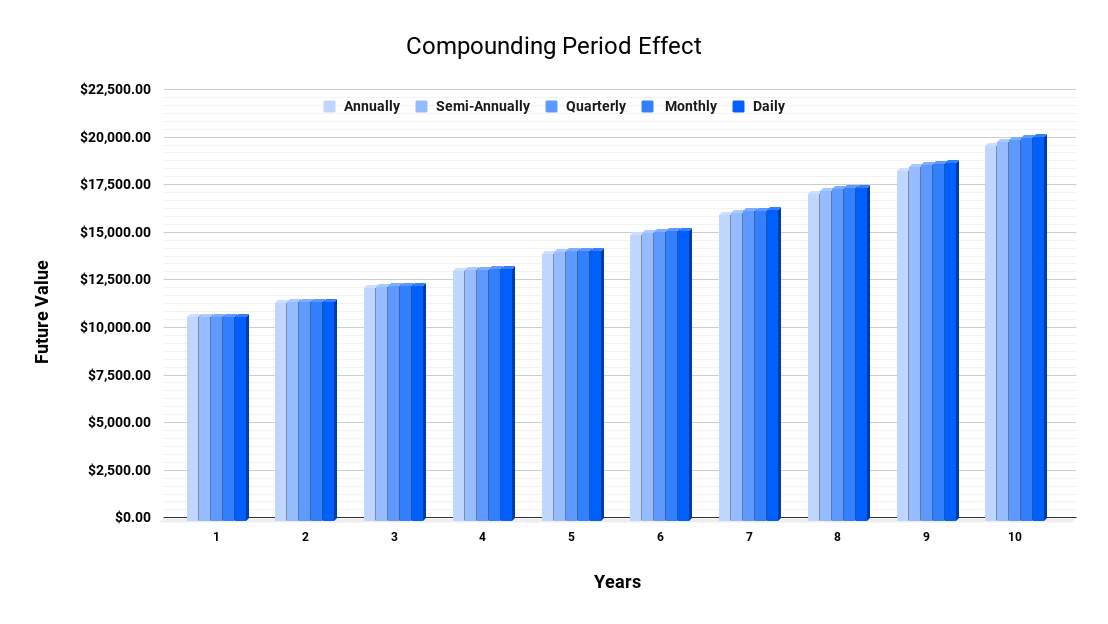
More frequent compounding periods means greater compounding interest, but the frequency has diminishing returns. This example shows the interest accrued on a $10,000 investment that compounds annually at 7% for four different compounding periods over 10 years.
Compound Interest Formulas
1. Compound Interest Formula (simple)
This is the simple compound interest formula including initial deposit:
A = P * (1 + r/n)n*t
To calculate the total compound interest generated we need to subtract the initial principal:
I = P * (1 + r/n)n*t - P
2. Compound Interest Formula (with regular deposits)
Compound interest for principal equation
A = P * (1 + r/n)n*t
Future value of a series formula - end of period
A = PMT * (((1 + r/n)n*t -1) / (r/n))
Note: the formula above assumes deposits are made at the end of the period (end of month, year, etc.)
Future value of a series formula - beginning of period
A = PMT * (((1 + r/n)n*t -1) / (r/n)) * (1 + r/n)
Note: the formula above assumes deposits are made at the beginning of the period (end of month, year, etc.)
3. Compound Interest Formula (with different periodic payments)
Compound interest for principal equation
A = P * (1 + r/n)n*t
Future value of a series formula - end of period
A = PMT * pf * (((1 + r/n)n*t -1) / (r/n))
Legend:
- A = future value of investment including interest (amount)
- P = principal investment amount (initial deposit)
- r = nominal annual interest rate (as a decimal)
- t = the overall length of time the money is invested for and interest applied for
- n = compounding frequency per unit of time t
- I = total compound interest
- PMT = the monthly payment / deposit
- pf = the payment frequency in the compounding period
4. Rule of 72
The Rule of 72 is a simpler way to determine how long it'll take for a specific amount of money to double, given a fixed return rate of return that is compounded annually. It can be used for any investment, as long as there is a fixed rate that involves compound interest. Simply divide the number 72 by the annual rate of return and the result of this is how many years it'll take.
As an example, $1000 with a fixed rate of return of 7% will take around 10 (72 divided by 9) years to become $2000.
Keep in mind that the Rule of 72 disregards any fees / commissions or taxes paid on investment gains. It is generally used only as a rough guideline when you need a quick number.
5. Google Sheets - Compound Interest Function
FV - The FV function calculates the future value of an annuity investment based on constant-amount periodic payments and a constant interest rate.
FV(rate, number_of_periods, payment_amount, [present_value], [end_or_beginning])
- rate - The interest rate.
- number_of_periods - The number of payments to be made.
- payment_amount - The amount per period to be paid.
- present_value - [ OPTIONAL - 0 by default ] - The current value of the annuity.
- end_or_beginning - [ OPTIONAL - 0 by default ] - Whether payments are due at the end (0) or beginning (1) of each period.
Compound intererest Frequently Asked Questions
What are the most common compounding periods?
In practice, banks and other investments vehicles use yearly, quarterly and monthly compounding periods, in that order. Banks generally provide saving accounts with yearly capitalization of the interest while investments in stocks that pay a dividend have yearly, quarterly or monthly payments.
When is interest compounded?
In general, for savings accounts, interest can be compounded at either the start or the end of the compounding period (this is usually every month or every year). If additional contributions are included in your calculation, the compound interest calculator will assume that these contributions are made at the start of each period.
What is the effective interest rate?
The effective interest rate (or effective annual rate) is the rate that gets paid after all the compounding. When compounding of interest takes place, the effective annual rate becomes higher than the overall interest rate. The more times the interest is compounded within the year, the higher the effective annual rate will be.
Are the results of the compound interest calculator shown in today's value?
The results of this calculator are shown in future value of the money. If you turn on the "Inflation (%)" option, then you can also see the adjusted for inflation value as well.
References
- Wikipedia - Compound Interest & Effective Interest Rate
- Investopedia - The Rule of 72 Defined & Compound Interest
- University of Baltimore - Mathematics of Money - Compound Interest Analysis With Applications
- Google Sheets - FV - Docs Editors Help
Whilst every effort has been made in developing this compound interest calculator, we are not to be held liable for any special, incidental, indirect or consequential damages or monetary losses of any kind arising out of or in connection with the use of the calculator and information derived from this web site. This calculator is here purely as a service to you. Your use of them is at your own risk. The calculations results given by the compound interest calculator serve only as guide for potential future value. Please speak to an independent financial advisor for professional guidance.